مجموع ارقام (مرحله اول بیست و هفتمین المپیاد ریاضی- سوال 22):
مجموع ارقام کدام یک از اعداد زیر بیشتر است؟
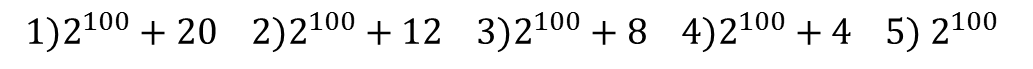
پاسخ: 2) 12 + 2100
برچسب ها : مجموع ارقام ,

مجموع ارقام (مرحله اول بیست و هفتمین المپیاد ریاضی- سوال 22):
مجموع ارقام کدام یک از اعداد زیر بیشتر است؟
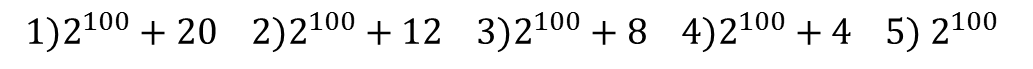
پاسخ: 2) 12 + 2100
نت موسیقی (مرحله اول بیست و سومین المپیاد کامپیوتر- سوال2):
می خواهیم آهنگی با نت های موسیقی بسازیم با ین شرط ها که فقط از نت های "سل"، "لا" و "سی" استفاده کنیم، بعد از هیچ نت "سل"ای بلافاصله نت "سی" نیاید و طول آهنگ دقیقا سه نت باشد. با فرض اینکه می توان از نت های تکراری استفاده کرد به چند طریق می توان چنین آهنگی ساخت؟
1) 9 2)15 3)24 4)21 5)27
پاسخ: 4) 21
با توجه به فرمولی که در مطالب قبل داده ایم، این مسئله را حل می کنیم:
فرمول:
تعداد n عدد با تکرار:
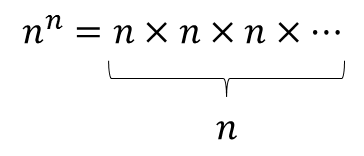
تعداد n عدد بدون تکرار:
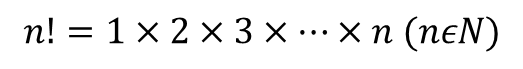
پس تعداد آهنگ های 3 نتی که بدون شرط می توان با 3 نت ساخت، 27 است.
حال تمام حالت هایی را که "سی" بعد از "سل" بلافاصله آمده می نویسیم:
سل-سی-لا _ سل-سی-سی _ لا-سل-سی _ سی-سل-سی _ سل-سل-سی _ سل-سی-سل
برای آسانی کار بهتر است به جای نت ها از a ,b ,c استفاده کنیم. (سل=a، لا=b، سی=c)
acb, acc, bac, cac, aac, aca
تعداد نت های غیر قابل قبول 6 تا است. --> 27-6=21
همیشه این روش جواب می دهد و استفاده از کلمات سخت و طولانی می باشد و نیاز به فسفر بیشتری است. در ضمن استفاده از کلمات ممکن است شما را گیج و متحیر سازد.
سرشماری (مرحله اول سی و یکمین المپیاد ریاضی- سوال 1):
مامور آمار، یک سرشماری در شکرستان انجام داده است. فراوانی نسبی تعداد خانواده ها به صورت زیر است:

چند درصد از مردم، در خانواده های 2 نفری زندگی می کنند؟
پاسخ:
در وهله اول باید تعداد افراد شکرستان را بدانیم. پس اعداد اعضاء را در درصد ضرب می کنیم.

مجموع افراد شکرستان 400 نفر و مجموع خانواده های 2 نفری 20 نفر است. حال باید تناسب برای مشخص کردن درصد بگیریم.

اعداد و بخشپذیری (مرحله اول سی و یکمین المپیاد ریاضی- سوال 3):
چند عدد چهار رقمی با ارقام 1، 2، 3، 4 وجود دارد که هیچ کدام از رقم های آن تکرار نشده باشد و مجموع هر دو رقم متوالی آن بر 2 یا 3 (یا هردو) بخشپذیر باشد؟
پاسخ: 2 رقم (3124 و 4213)
در شروع باید بفهمیم که با چهار عدد a و b و c و d چند عدد چهار رقمی می توانیم بسازیم. دو حالت کلی داریم:
الف- با تکرار: با توجه به فرمول به جای n تعداد ارقام را می گذاریم.
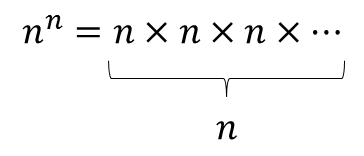
ب- بدون تکرار: با توجه به فرمول به جای n تعداد ارقام را می گذاریم.
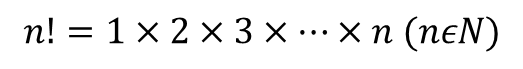
ab, bc, cd/2, 3 --> n! = 1.2.3 = 6 --> ab, bc, cd = 12, 21, 13, 31, 24, 42
البته اگر مسئله اعداد دیگری مانند 5 و 6 و 7 و 8 را داده باشد، سوال و تحلیل متفاوت خواهد بود.
بخش پذیری (مرحله اول سی و یکمین المپیاد ریاضی کشور- سوال 16):
جمع صورت و مخرج چند تا از کسرهای ( 1/90 , 2/90 , 3/90 , … , 90/90) بعد از ساده کردن بر 3 بخشپذیر است؟
پاسخ: 3 کسر (9/90 , 18/90 , 45/90)
اول باید از 1 تا 90 تمام مقسوم علیه های 90 را پیدا کنیم.
{A(90) = {1,2,3,5,6,9,10,15,18,30,45,90
حال باید اعدادی را دو به دو باهم جمع بزنیم که بر 3 بخشپذیر هستند.
مثال: {1+2, 1+5, 2+10, 3+6, …} = B
این کار را تا آخرین عدد انجام می دهیم. این اعداد ساده ترین حالت صورت و مخرج است. برای مثال 2+1 را در نظر می گیریم. حال عدد بزرگتر را مخرج و عدد کوچکتر را صورت در نظر می گیریم و به صورت رو به رو عمل می کنیم.
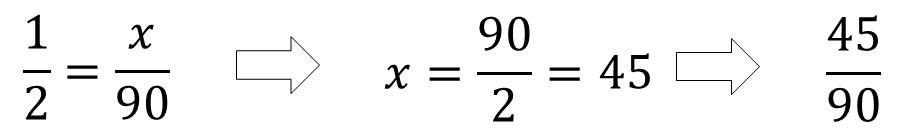
حال اعداد مجموعه B را به همین صورت در برابری مخرج 90 قرار می دهیم و X را بدست می آوریم.