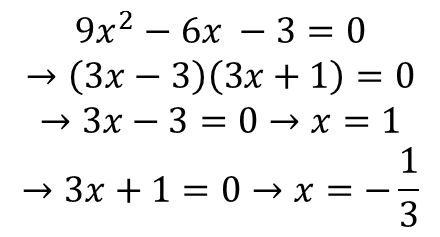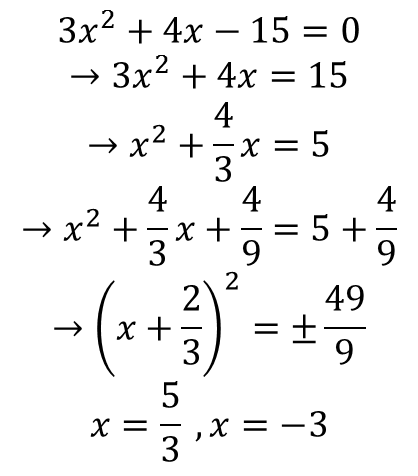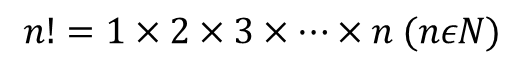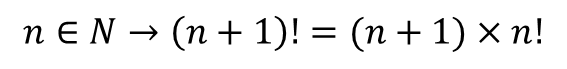معادله درجه دوم:

·        روش هندسی (سهمی):

نمودار رابطه y=x² که آن را سهمی می نامیم به صورت زیر است:

1. خط تقارن این سهمی محور عرض، و رأس سهمی مبدأ مختصات است.

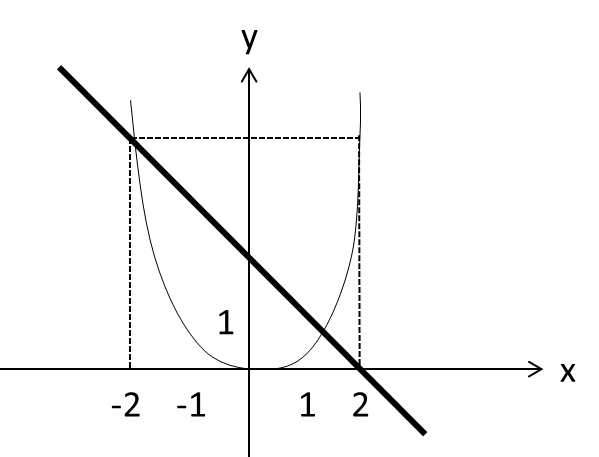
2. معادله x²+x-2=0 را در نظر بگیرید. می توان گفت جواب این معادله طول نقاط برخورد سهمی y=x² و خط y=-x+2 می باشد.

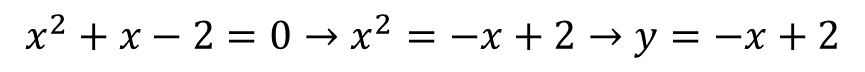
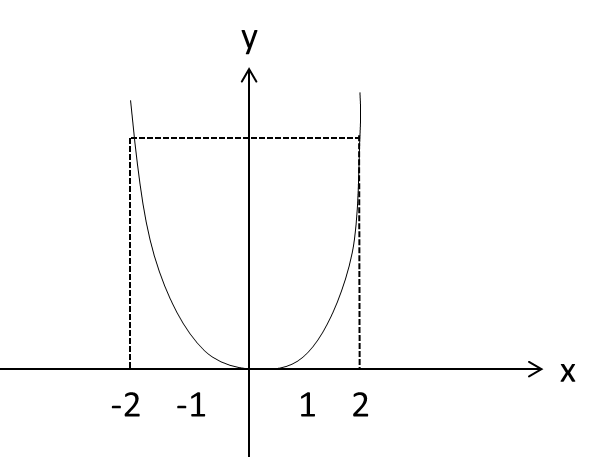
3. روی نمودار ملاحظه می کنیم خط y=-x+2 سهمی y=x² در نقاط (1,1) و (-2,4) قطع می کند که طول این نقاط یعنی 1 و -2 جواب های معادله x²+x-2=0 می باشند.

ادامه مطلب...




برچسب ها : معادله درجه دوم (روش هندسی)  ,

معادله درجه دوم:

·        تجزیه: سه جمله ای را به صورت حاصلضرب دو پرانتز تجزیه می کنیم و هر کدام را برابر صفر قرار می دهیم. سپس x را حساب می کنیم. (مثلا a×b=0 است؛ مطمئنا یکی از ایندو یا هر دوی آنها برابر صفر است.)

·        مربع کامل:

1. جملات مجهول را در یک طرف تساوی و عدد ثابت را طرف دیگر قرار می دهیم.

2. اگر ضریب x²غیر از یک است، طرفین را بر این ضریب تقسیم می کنیم.

3. مربع نصف ضریب x را به دو طرف معادله می افزاییم تا یک طرف مربع کامل شود.

4. در صورتی که دو طرف مثبت باشند از طرفین جذر می گیریم.

ادامه مطلب...




برچسب ها : معادله درجه دوم (3 روش)  ,

فاکتوریل (!):

در فاکتوریل قوانین خاص است؛ یعنی نمی توان برای یک رابطه که در فکرمان است، یک رابطه دقیق نوشت.

قرارداد:   0!=1

دلیل این قرارداد این است که فرمول هایی داریم که به ازاء اعداد طبیعی کوچکتر یا مساوی n برقرار است و برای برقراری آنها به ازاء صفر ناچاریم 0! را برابر یک قرار دهیم.

فاکتوریل یک تعریف بازگشتی است؛ یعنی برای یافتن فاکتوریل یک عدد طبیعی داشتن مقدار فاکتوریل عدد قبل از آن لازم است.

گاهی اوقات لازم است به جای محاسبه حاصلضرب اعداد 1 تا (با) n شاید لازم باشد حاصلضرب اعداد n تا (با) 1 را در نظر بگیریم.

مثال:

3 = !2 + !1 = !(1+2)

18 = 6 - 24 = !3 - !4

2 = !2 × !1 = !(2×1)

8 = !7 ÷ !7 × 8 = !7 ÷ !8

هیچ یک از نتایج زیر یک حالت کلی نیست؛ پس نمی توان همیشه در فاکتوریل حالتی کلی یافت.

!m + n)! = m! + n)

!m – n)! = m! – n)

!m × n)! = m! × n)

!m ÷ n)! = m! ÷ n)

مجذور غیر کامل (مرحله اول سی و یکمین المپیاد ریاضی- سوال10):

حداکثر چند عدد از میان اعداد طبیعی 1 تا 1391 می توان انتخاب کرد که ضرب هر دوتایی از آن ها مربع کامل باشد؟

پاسخ: 37

با گرفتن جذر 1391 (=37/29) می فهمیم که آخرین مجذور کامل 37 است.

راه های بدست آوردن جذر:

1. تجزیه: با تقسیم اعداد بر عوامل اول از کوچکترین عدد اول.

2. حدس و گمان: با حدس یک عدد و مجذور کردن آن این کار را می کنیم.

3. جذر گیری: مراجعه شود به کتب راهنمایی.

اعداد پنج رقمی (مرحله اول بیست و هفتمین المپیاد ریاضی- ویراسته):

چند عدد پنج رقمی با ارقام {1،2،3،4،5} وجود دارد که ارقام آن متمایز باشد و مجموع رقم اول و رقم پنجم با مجموع رقم دوم و رقم چهارم برابر باشد؟

الف) 8   ب) 12   ج) 16   د) 24   ه) 36

پاسخ: د) 24

فرض می کنیم که عدد ما به صورت abcde است.

جزئیات: a+e=b+d

به هشت صورت می توان این رابطه را نوشت:

        ·            a+e=b+d --> aecbd

        ·            a+e=d+b --> aecdb

        ·            e+a=b+d --> eacbd

        ·            e+a=d+b --> eacdb

        ·            b+d=a+e --> bdcae

        ·            b+d=e+a --> bdcea

        ·            d+b=a+e --> dbcae

        ·            d+b=e+a --> dbcea

نتیجه می گیریم که در عدد abcde هر رابطه a+e=b+d ، ما 8 عدد پنج رقمی با اعداد متمایز دارد.

در اعداد {1،2،3،4،5} رابطه (abcde) --> (a+e=b+d) را به سه صورت داریم:

        ·            4+2=5+1

        ·            3+2=4+1

        ·            4+3=5+2

برای هر رابطه 8 عدد داریم؛ پس در کل 24 عدد به این صورت داریم.