اعداد و بخشپذیری (مرحله اول سی و یکمین المپیاد ریاضی- سوال 3):

چند عدد چهار رقمی با ارقام 1، 2، 3، 4 وجود دارد که هیچ کدام از رقم های آن تکرار نشده باشد و مجموع هر دو رقم متوالی آن بر 2 یا 3 (یا هردو) بخشپذیر باشد؟

پاسخ: 2 رقم (3124 و 4213)

در شروع باید بفهمیم که با چهار عدد a   و b و c و d چند عدد چهار رقمی می توانیم بسازیم. دو حالت کلی داریم:

الف- با تکرار: با توجه به فرمول به جای n تعداد ارقام را می گذاریم.

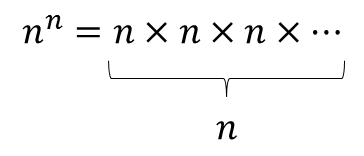
ب- بدون تکرار: با توجه به فرمول به جای n تعداد ارقام را می گذاریم.

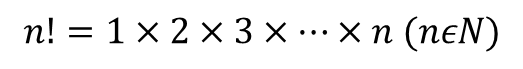
ab, bc, cd/2, 3 --> n! = 1.2.3 = 6 --> ab, bc, cd = 12, 21, 13, 31, 24, 42

 البته اگر مسئله اعداد دیگری مانند 5 و 6 و 7 و 8 را داده باشد، سوال و تحلیل متفاوت خواهد بود.