اتحاد ها (1):

·        اتحاد اولر:

اگر a و b و c سه عدد حقیقی باشند، داریم:

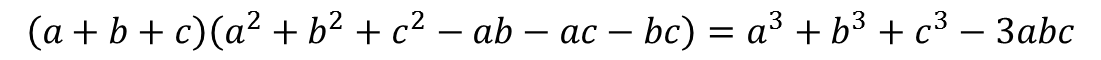
صورت دیگر اتحاد اولر:

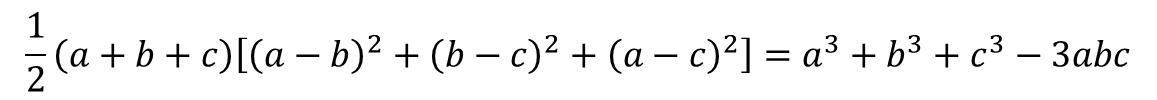
نتایج:

1. اگر a + b + c = 0 آن گاه a³ + b³ + c³ = 3abc

2. اگر a = b = c آن گاه a³ + b³ + c³ = 3abc

مثال: معادله (1 – x)³ + (2x + 4)³ – (x + 5)³ = 0 را حل کنید.

(1 – x)³ + (2x + 4)³ – (x + 5)³ = 0

-->(1 – x)³ + (2x + 4)³ + (-x - 5)³ = 0

-->(1 – x)³ + (2x + 4)³ + (-x - 5)³ = 3 (1 – x) (2x + 4) (-x - 5) = 0

--> 1 – x = 0 --> x = 1   ,    2x + 4 = 0 --> x = -2   ,   -x – 5 = 0 --> x = -5

نکته: چون توان – (x + 5)³ فرد است؛ مطمئنا می توان منفی یک را در (x + 5)ضرب نمود.

·        اتحاد دو جمله ای n درجه:

به این صورت زیر داریم:

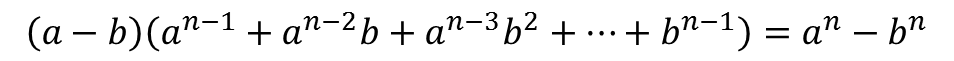
اما در صورتی که n عددی فرد باشد، آنگاه:

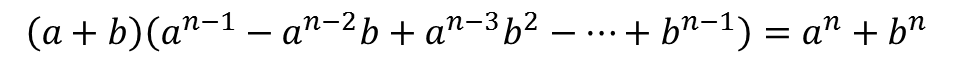
نکات:

1. aⁿ – bⁿ همواره بر a – b بخش پذیر است.

2. اگر n عددی زوج باشد aⁿ – bⁿ بر a + b بخش پذیر است.

3. اگر n عددی فرد باشد aⁿ + bⁿ بر a + b بخش پذیر است.

4. aⁿ + bⁿ بر a – b بخش پذیر نیست.

مثال: عبارت 16a⁴ – 81b⁴ را تجزیه کنید و امتحان کنید که عبارت aⁿ – bⁿ بر a – b و گاهی بر a + b بخشپذیر است.

--> 16a⁴ – 81b⁴ = (2a – 3b) (8a³ + 12a²b + 18ab² + 27b³) 

--> 16a⁴ – 81b⁴ = (4a² + 9b²) (2a + 3b) (2a – 3b)

--> (4a² + 9b²) (2a + 3b) (2a – 3b) ÷ (2a + 3b) = (4a² + 9b²) (2a – 3b)

--> (4a² + 9b²) (2a + 3b) (2a – 3b) ÷ (2a – 3b) = (4a² + 9b²) (2a + 3b)